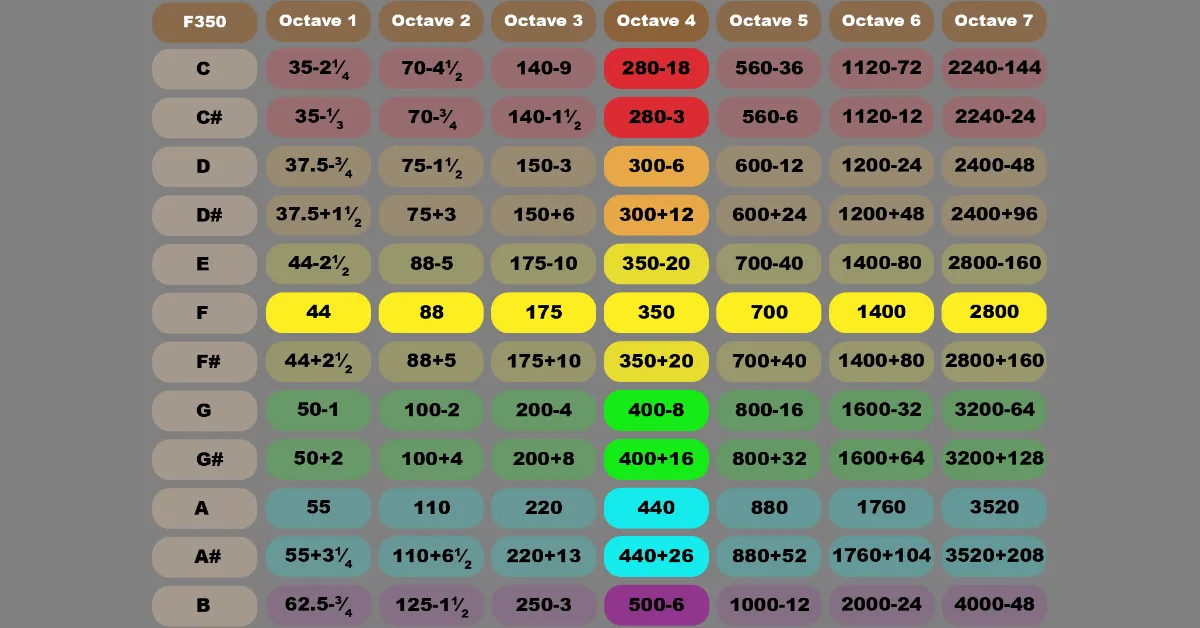
We’ve all sat down and tried to memorize the audio frequency chart. I don’t know how it went for you but it didn’t go well for me. That is, until I woke up one morning and had a vision which changed everything.
The F350 Method for memorizing the audio frequency chart is based on six whole numbers and ten offsets which are easy to divide and multiply. If you can do third grade math then you can use these sixteen numbers, fourteen actually since three of them are the same, to memorize all 10 musical octaves with at least a 99.2% accuracy – or greater. Everyone knows A=440, right? Well, guess what? F4=350, E4=350-20 and F#=350+20. Just double these numbers as you go up in pitch and half them when you go down in pitch while maintaining whether it’s addition or subtraction. Easy As F350!
[Super Simple Shortcut: Memorize Octave 4 and use a calculator to figure out the other octaves. -Michael 20230911]
Perhaps You Had Better Start From the Beginning…
Like I mentioned at the beginning, I have wanted to memorize the audio frequency chart since I learned about it. I had heard about harmonic mixing for DJing and EQing while mixing and thought it’d be a valuable skill to have. The problem is that there are almost 120 separate values and most of them have decimals to the one hundredths place. This is no simple times table from third grade – this is information warfare!
So I remembered that I had taken the Mega Memory course and proceeded to use those hacks. I thought that I’d start with an audio frequency we can actually hear and C1 seemed like a good note on which to start. The first value I learned was 32.7Hz. The way I memorized it was by visualizing a carrot, which represented the note C, a tray that represented the number three, hitting said carrot with the tray and throwing up a peace sign for deuce, pointing at the carrot as it flew away (which represented the point) and then being shocked when the carrot turned into a Seagram’s 7 bottle.
Shockingly, it actually kind of worked. I proceeded to add another number – C2 – which is 65.41Hz. That’s when the problem became clear: there are too many dag-gone numbers! That brought me to the concept of ‘offsets’. Since 32.5 is easily multiplied to 65, I could just add 0.2 to the first number and then 0.4 to the second and so on. But then I had a vision which would change my musical note frequency memorizing life forever.
Vision of the Musical Future
You know how sometimes when you wake up, you aren’t sure whether you’re awake or not? It’s kind of a lucid dreaming-type state and that’s what happened to me. The first thing I saw was two nerdy kids across from a table from one another with their laptops. The skinnier, more confident, one was explaining to the other that some famous DJ said that the song they were about to play together was in the key of 7774Hz. “Yeah right, Ableton,” I thought to myself, “That’ll never happen. People name keys by note name, not audio frequency.” Did I mention it was an Ableton Live ad? Dreams are weird.
Directly following that, another image came into my brain. This time it was a chart populated by two notes: 32.5 and 65. They were written in a clear, bold font and communicated simplicity. “Yes,” my inner dialog went, “people can only remember halves – not odd decimals.” It was at this point that I realized that I could teach this to people.
Given the ubiquitous nature of home recording as well as music-creation apps being available to everybody on mobile devices, the need for musical note frequency literacy is at an all-time high. Imagine being able to use any EQ – not just those with frequency readouts – and know with a 99.2% certainty that you’ve dialed in the exact note you want. How much more confident would you be in your mixing skills? I’d say a lot more confident.
Show Me The Audio Frequency Chart
Alright. You’ve made it this far which means you are really curious about the F350 Method. Before I show you the F350 chart, I want to show you a conventional frequency chart and trigger your PTSD.

Unless you’re some kind of mathematical genius, there’s no way you’re memorizing this audio frequency chart without some help. However, if you look closely, you’ll notice that one row of numbers stands out: the ‘A’ row – they’re all whole numbers. Well, of course they are – pitch reference is a man-made creation. Even so, you’ll also notice that there are other whole numbers such as G4, F#4, G3 and G2. There are also several which are really close to being whole numbers. Look even more closely and you’ll see there are plenty of perfectly half numbers – particularly in the Zero Octave audio frequencies – more on that later.
Introducing: The F350 Method
Before I unveil the full F350 Method graph, let’s first look at the six base numbers which make it possible. By doing this, you’ll be introduced in a step-by-step manner that won’t overwhelm you. Remember how I said that there are already some whole numbers and others are very close? Take a look at this:
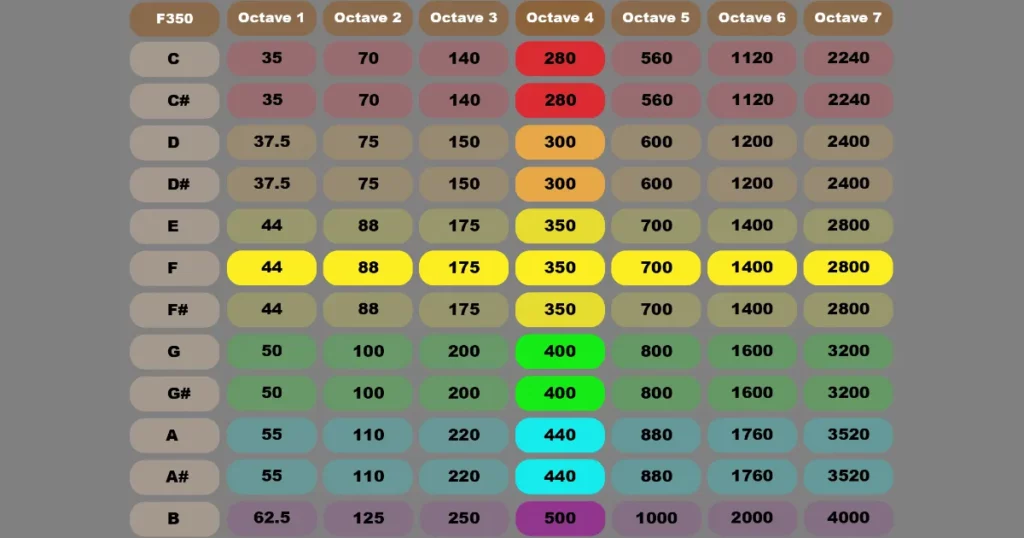
Compare this graph to the previous one. You’ll note that these numbers are really close. One is the same, A4=440, and one is used three times, F4=350. Besides B4, which is 500, the rest are value which sit somewhere between the actual ones. I call this the F350 Method because everyone already knows that A4=440Hz but not everyone knows that F4 is very close to 350Hz and the number 350 is used three times and is the center of the whole fabric.
Another thing to note is that all the numbers change by 50 except for 440 and 280. Again, everyone knows A440 and 280 was the best I could do for the C group. It’s worth mentioning that F4, F#4 and E4 all use the number 350 as their base. All other ‘letters’ get their own number. Everything is in sharps because that’s how most digital audio workstations present accidentals. Note how easy every number is to multiply and divide.
The 88 Exception
There is one special rule. I initially wanted to call this the ‘Easy AF Method for Memorizing The Audio Frequency Chart’. Consequently, I did everything I could to make it ‘Easy AF’. You can see that for the E, F and F# group, 88 isn’t actually half of 175. I did this because it’s easier for me to remember and use. The difference in accuracy it makes is literally just 0.52%. With the offsets, which you’re about to see, the entire accuracy of this system is 99.20% or greater – 100% to the hundredths place in some cases. If you’re good at math and know that half of 175 is 87.5 and half of that is 43.75 then, by all means, enjoy an accuracy of 99.72%. For the rest of us, half of 175 is 88. Now behold the rest of the audio frequency octaves including offsets:
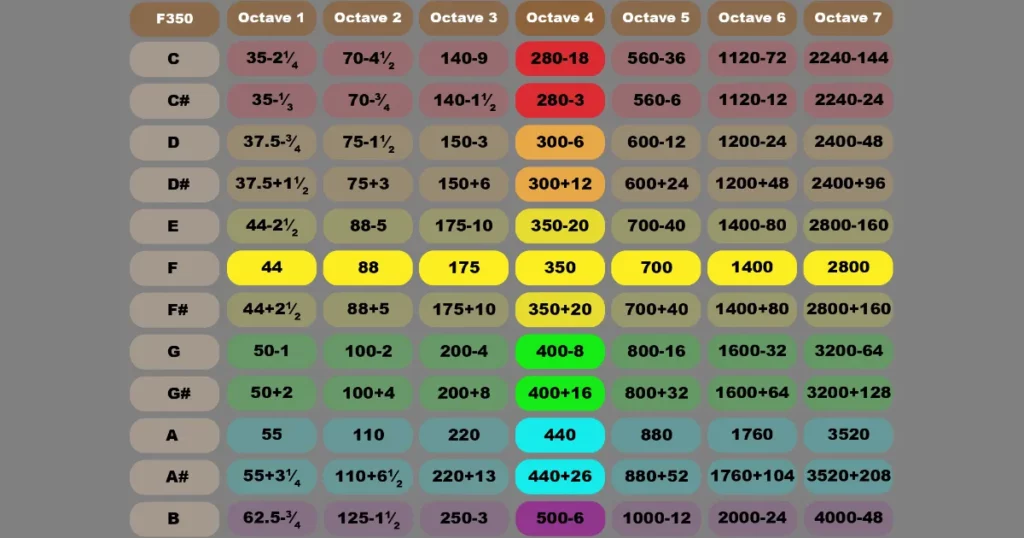
Now before you say, “WTF?!” and close this tab: stay with me. This is as ‘Easy AF’ as I could make it. I have searched Google and there is nobody showing this method of memorizing the audio frequency chart. All everyone else shows are regurgitated precision values which practically nobody has ever retained. I memorized this in a day and so can you. Give me five minutes of your time and you can memorize at least eight audio frequency octaves to my promised minimum of 99.20% accuracy and never have to look at an audio frequency chart again.
Offset Adventure
Here’s the explanation: there are ten offsets and two of them are the same number. The rest are grouped by note name. Here’s the 350 group:
- E4 is 350-20
- F4 is 350
- F#4 is 350+20
Pretty easy right? This group of three notes all use 350 as the base and have an offset of 20. F4 is 350, E4 is 350-20 and F#4 is 350+20. The next group of offsets are mathematically related to their base number:
- D4 is 300-6
- D#4 is 300+12
So 300 is 50 less than 350. Makes sense since D is lower than E. The offsets work like this: 6 is 3×2, which you can remember because they’re part of the 300 group, and 12 is 3×4. D is lower than D# so you subtract 6 for D and add 12 for D#. The next group is pretty much the same but with higher numbers:
- G4 is 400-8
- G#4 is 400+16
This works exactly like the D group except with 400 as the base. Again, the base number is 50 more than 350 and the offsets are related to that number in the same way as the D group. 4×2 is 8, 4×4 is 16. You subtract 8 from 400 to get G4 and add 16 to 400 to get G#4. Easy peasy. The next group I’ll show you is the A group. Since everyone knows that A4=440, and because it’s easier to divide and multiply, I used that number as a base instead of 450:
- A4 is 440
- A#4 is 440+26
While this offset isn’t directly related to the base number, it’s simple to multiply and divide. Two more groups to go! The B group is super easy since the base number is 500:
- B4 is 500-6
The cheese stands alone on that one. I think that base number is the easiest of all. Everyone can multiply and divide 500! Lastly, the C group which uses 280 as its base:
- C is 280-18
- C# is 280-3
I realize that this one is a little different. Not only are the numbers not related to the base number, neither are they really related to each other. That being said, these numbers are easy to multiply and divide and saying, “two-eighty minus eighteen” kind of rhymes. 280 is also similar to 440 which is the other base number which isn’t an even 50.
But Muh Octaves
By now you might be wondering, “What’s all this with the Fourth Octave? I want bass, bro!” I feel ya, m8. While I don’t remember all the steps I went through in creating this – indeed it kind of just came to me – there were a few guiding principles which were inspired by my mixcube speaker. One of them was keeping it ‘Easy AF’ – which I think we’ve accomplished. Another was not wanting to start from either end of the audio frequency spectrum and having to go through all the octaves every time. The last principle is in support of bass accuracy.
Since the lower the pitch, the closer the audio frequencies are to one another, I realized that I had to prioritize for the lower octaves to be more accurate. Strangely, all the octaves are more or less as accurate as any other. But since you want to know how to calculate the other octaves, let me tell you.
Stairway to Audio Frequency Hell
All you do to get higher and lower octaves is just multiply or divide both numbers by 2 and keep whether the offset is added or subtracted. Let’s use F4=350 as our first example, since it has no offsets.
- Going Up: F4=350, F5=700, F6=1400, F7=2800
- Going Down: F3=175, F2=88, F1=44
Remember that I use 88 as half of 175 for simplicity while only sacrificing 0.52% accuracy. This is the only place I do this (actually I do similar rounding for C#1) – but you don’t have to! Now let’s look at E:
- Going Up: E4=350-20, E5=700-40, E6=1400-80, E7=2800-160
- Going Down: E3=175-10, E2=88-5, E1=44-2½
You can see that you just multiply both the base number and the offset by 2 then combine them to go up and divide them each by 2 then combine them to go down. Finally, let’s look at A# for an example using addition:
- Going Up: A#4=440+26, A#5= 880+52, A#6=1760+104, A#7=3520+208
- Going Down: A#3=220+13, A#2=110+6½, A#1=55+3¼
Extended Range
You can use this basic F350 Method to go down to the Zero Octave or beyond the Seventh Octave. The reason I don’t show it on the graph is threefold: 1. three octaves in either direction is usually plenty since you can’t hear most of the Zero Octave and everything past the Seventh Octave is sibilance and harmonics, 2. I’m not a math professor and it’s honestly hard for me to even multiply 26×2 and, 3. I have a separate system for the Zero Octave which, when taken in consideration with the other two factors, made me leave it out of this chart. That being said, this chart – especially if you can divide 175 by 2 and that in 2 again – is the slightly more accurate option.
Audio Frequency Bottom Feeder
Which leads me to the basement audio frequencies, the Zero Octave, the notes you can’t hear and your speakers can’t reproduce anyway. This isn’t sub bass – this is bass below bass; rumble. If Dante wrote a book about audio, he’d start here – in the sonic inferno.
Despite these facts, I know many of you – myself included – yearn for completion. What good is a system that doesn’t cover every possibility – complete with options – however seldom-used? It isn’t good for diddly squat, that’s what.
So, for you Sultans of Shake, Lords of the Low, and church organists, I present to you ‘The Zero-Octave Sweet 16 Rule’ and it goes a little something like this:
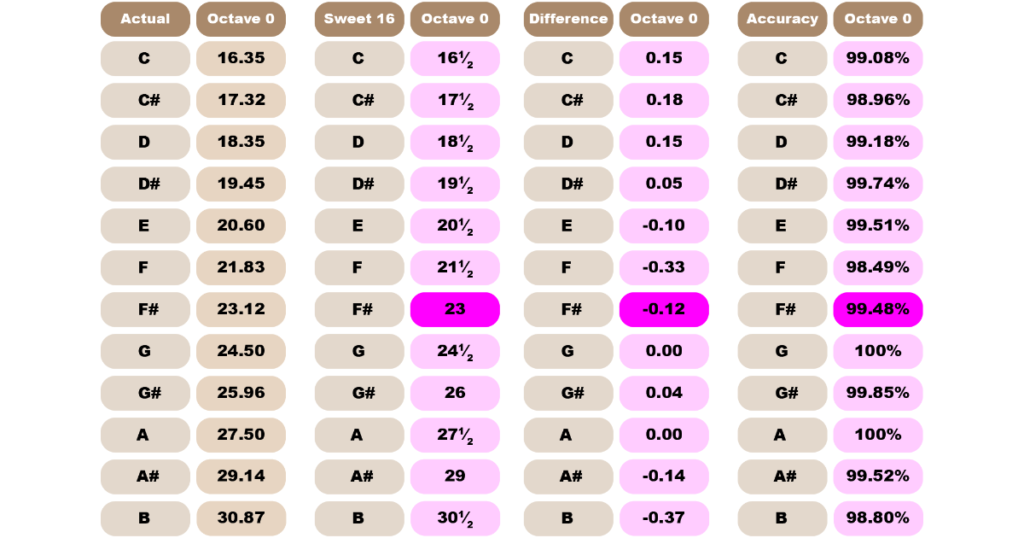
Oh, boy. How do I explain this one? Just kidding – it’s easy AF. It’s called Sweet 16 because C0 is 16½. In fact, all the numbers are halves from 16-21. The phrase I use to remember this is, “16-21, half as fun.” Come on, you can’t smoke until you’re 21 – at least in California – and what fun is that?
In any case, remember that movie The Number 23 with Jim Carrey? Well F# is that number almost exactly. What, with all this audio frequency number madness, that should be easy enough to remember. The rest of the Zero Octave values go up by 1½. What’s that? Not accurate enough for you? Fixed:
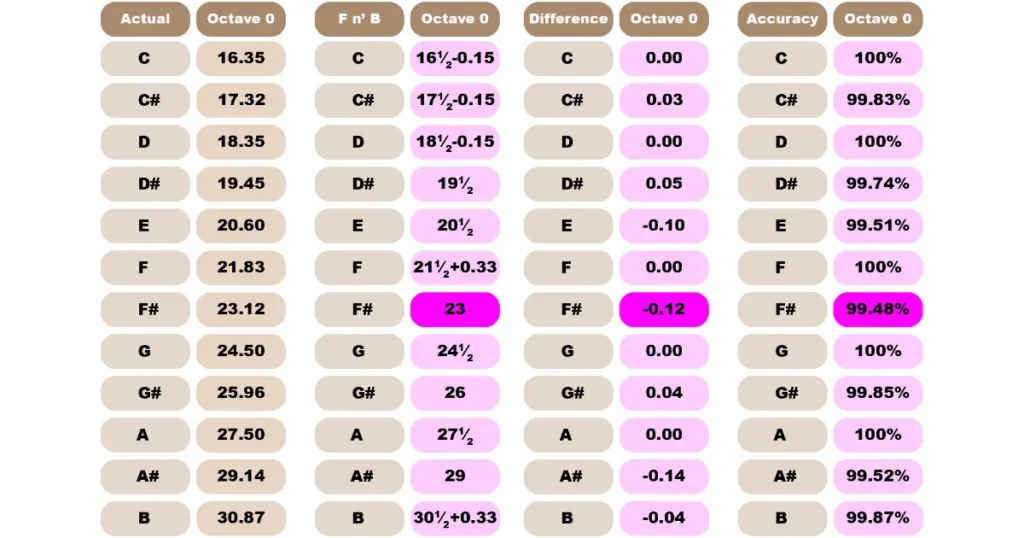
Sweet sixteen, an F’n B: just add point 33. First three subtract point fifteen! Slightly more accurate overall.
Oh, great – more offsets. Come on, it’s easy! It’s still the same ‘Sweet 16 Rule’ except with a cheerful rejoinder: “F’n B add point 33, first three subtract point fifteen!” It rhymes with Sweet 16! Say it with me:
“Sweet Sixteen, an F’n B, just add point three three. First three subtract point fifteen!”
One more time for the folks in the back!
“Sweet Sixteen, an F’n B, just add point three three. First three subtract point fifteen!”
You know what it means when you politely call someone an ‘F’n B’, right? Well, there you go and it all rhymes.
Now, do you need this? No! You can use the F350 Method to find the Zero Octave audio frequency values and it’ll be more accurate. Then again, you don’t really need to know the Zero Octave anyway – unless you’re a church pipe organist and, be honest: you’re not. In any case, I can conceive of someone needing to know B0 so this is a handy and quick way of finding it. “Sweet 16, an F’n B…“
The Fact-Check is the New Trump Card
This isn’t a political blog but I do occasionally read the news. I understand the value of creating a reaction but I also appreciate accurate information. Since I know that since the beginning of audio, engineers and enthusiasts alike have struggled with this behemoth we call the audio frequency chart, it might come as a bit of a shock when I tell you that you can memorize the whole darned thing with just sixteen numbers. Am I right? Yes I am right, at least about the soundness of this method, and I can prove it. Arturo, bring out the Difference Graph por favor.
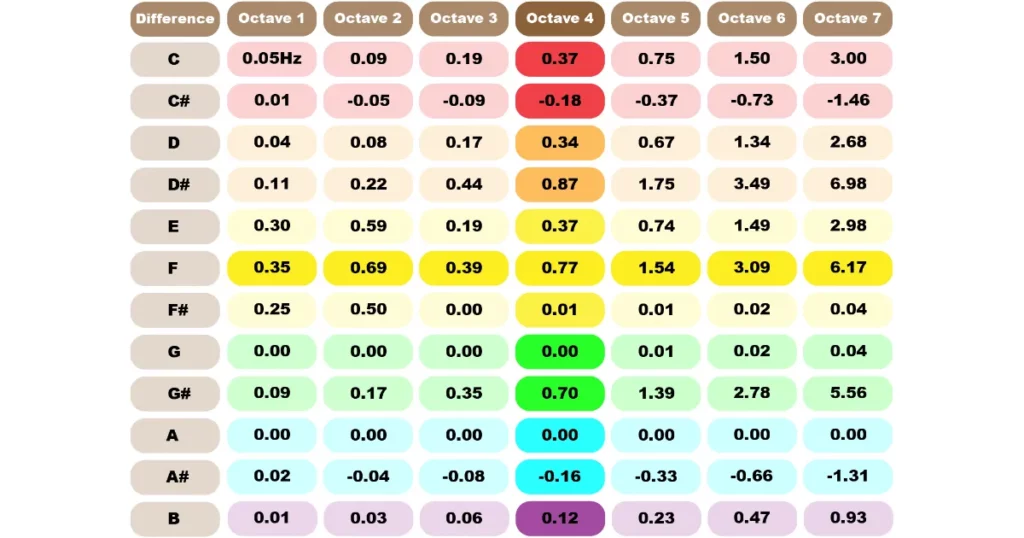
Before you soil your britches seeing that D#7 is almost 7Hz out, hear me out. I never said that this was 100% perfect – obviously that’s almost impossible and perfection hasn’t worked for us yet – but this method is better than you think. What you’re seeing above is a graph of the differences between the numbers which the F350 Method gives you and their pocket calculator audio frequency equivalents. Note all the 0.00 values – those that are not part of the A group are all accurate beyond one hundredth of 1Hz. I debated with myself about putting in values of ‘99.99+%’ but didn’t want to grunge up my pretty graphic.
You Hear That Audio Frequency?
Wikipedia says we can only hear to about a 5-6 cent accuracy. I’m sure that depends on the person, the listening environment and the octave in which the tested notes reside but if we take that fact at face value then almost none of these differences even matter. What I want to emphasize, though, is the precision which the lower octaves exhibit. Remember that I use 88 instead of 87.5 for the 350 group in the second octave for the ease of math so that affects the accuracy by 0.52%. Let’s look at the percentages next:
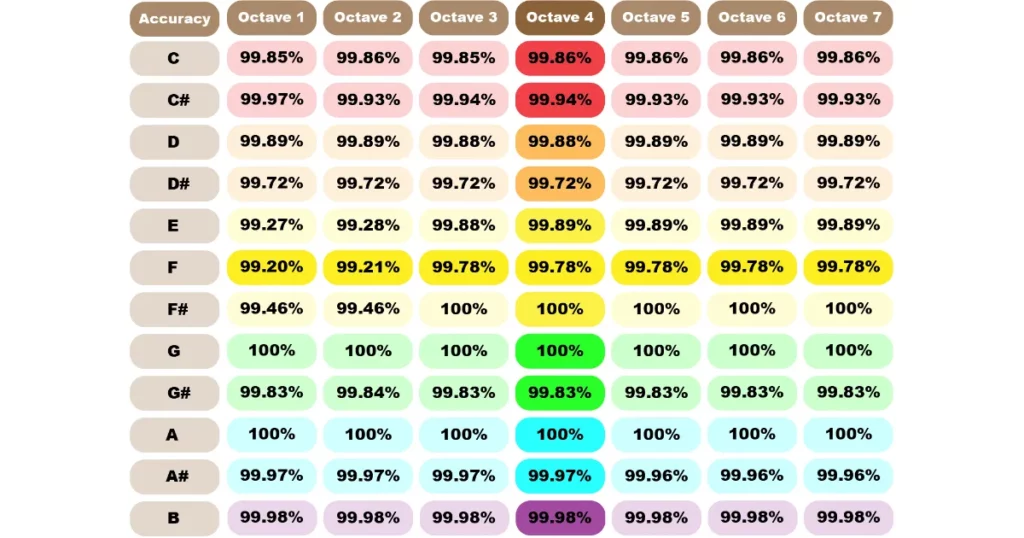
As you can tell from this graph, the least accurate value is F1 at 99.20%. For the fiftieth time, if you’re good at math then don’t use 88 as half of 175 and 44 as a substitute for 43.75 and the minimum accuracy of the F350 Method is 99.72%. I don’t know about you, but I’m happy with that.
Wielding The Weapon
The long and short of it is that, with nearly 10 octaves of audible notes – that’s 120 discreet values – most of which are not whole numbers, we don’t stand a realistic chance of memorizing all of them. However, if we simplify the data set and use values which are human-usable, I bet we can all get at least 99.20% there within a day – a week tops. Let’s explore some ways of memorizing this information before we part ways.
I highly recommend you use a keyboard for this. I centered everything around the Fourth Octave for a few reasons – one of which is because it’s easier to start from the middle and work your way out as opposed to starting at one end and constantly needing to count through every octave to get to where you want to go. This is definitely a different approach but every keyboard has Middle C, C4, so everyone with a keyboard can get started right away.
Starter Pack
I suggest beginning with F4=350 and remembering that E4 and F#4 also share the same base number. Practice going up and down three audio frequency octaves both ways and, before you know it, it’ll be second nature. Math savants can divide 175 into precise values and the rest of us can use 88 and 44. From there you can learn the groups on either side, the D group and the G group – both of which are 50 cents apart from the center. Go through and get used to multiplying and dividing those. Penultimately, remember that A4=440 – which you probably already know – and that the C group base number is 280. The last group, B, is 500 so that should pose you no challenge whatsoever.
Perhaps the most challenging thing about the F350 method is the offsets. Rest assured that if I, high school math certified as I am, can remember them then so can you. The center group is ‘Easy AF’ – +20 for F# and -20 for E. Divide by 2 going down, multiply by 2 going up – all the while maintaining whether you add or subtract.
The next group of offsets are related to the base number by 2 and 4. The 300/D group is -6 for D4 and +12 for D#4 and the 400/G group is -8 for G4 and +16 for G#4. The ‘A’ group only has one offset and that’s A#4 is +26 from A4’s base of 440. B4 is easy enough with it’s simple base of 500 and a minus 6 offset.
While the C group might be hardest to remember, the offset for C4 natural kind of rhymes with the base number: ‘two-eighty minus eighteen’. The offset for C#4 is -3 which is kind of related to -18 in that the 3 would make 18 into 15. I really don’t think it’s too hard, to be honest.
Off The Audio Frequency Charts
That’s it! Sixteen easily-memorable numbers which allow you to find at least seven audio frequency octaves – 10 or more if you want – with an accuracy of 99.20% or greater. I sincerely hope this was helpful and gives you greater confidence in your music-making adventures. If you like this, please share it with at least two people or on forums so it can spread. I really think this can revolutionize how we think of memorizing our note frequencies and I want everyone who’s ever desired doing so to have access to this.
You are now free to never look at a frequency chart again. Your mom will be so proud 🙂
Hexspa out!
20230911 Update: Hi, thanks for reading. Since uploading this in February 2019, I’ve used the F350 Method pretty regularly. Importantly, I only use the numbers from Octave 4 and use a calculator to figure out the rest. I suspect many of you either do or will do the same.
For example, if I want to know C9, I’ll say, “280-18=262 then multiply that by 2 five times. Not more than twice have I used the “Sweet 16 Rule”. That I think is best if you regularly find yourself in the Zero Octave. I just put a Super Simple Shortcut at the top of this page to reflect my present use of this method.
Ultimately, this is for you to use, mangle, remix, and/or develop as you see fit. I only ask one simple thing:
Remember who the OG is 🙂
Peace.